On TV recently I’ve been bombarded by adverts about the AXA Sun Life Guaranteed Over 50 Plan. The current version of the advert is presented by Michael Parkinson. Previous versions have been presented by June Whitfield.
I am no way near the age of 50 and these plans have no relevance to me. I should also point out that I am not a financial advisor, and am not intending to offer any opinion on these plans. My interest is to look at them from a simple mathematical point of view.
In case you’ve missed the advert the basic idea is this. If you are over 50 you can pay AXA a fixed monthly sum for the rest of your life. When you die a fixed sum (fixed at the time you open the plan) is payable to your family. If you die within two years you don’t get the fixed sum, but your family do get 1.5x your premiums back. If you ever stop contributing you don’t get anything.
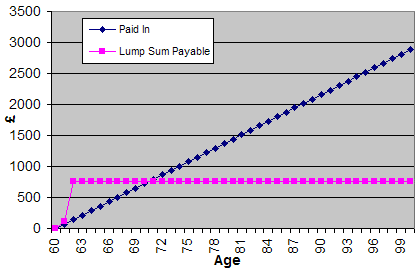
I went on their website and got a quote for a 60 year old male paying in £6 per month (the minimum a 60 year old male can pay in on the day I got the quote). This produces a cash lump sum of £760, payable on death after 2 years.
Here is a graph plotting how much you pay in, against how much you get back. You can see there is a cross-over point at which you end up paying in more money than you get back. In this case you end up having paid in more then you’d get out when you reach 71 years old.
The government publish data on life expectancy. I got the latest male life expectancy data from 2004 and 2006 and plotted this into another graph. Note how your life expectancy goes up as you get older. This is because you have already managed to avoid dying in the preceding years.
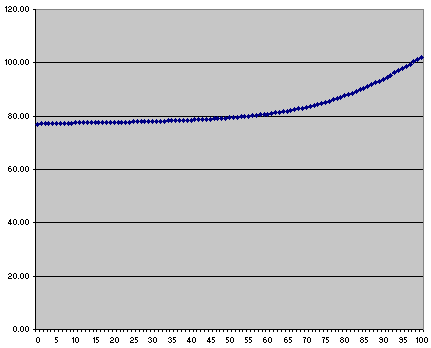
You might not be able to make out the detail on the graph but the life expectance for a 60 year old male in the UK is 80.81 years.
This means that if you are an average person you are likely to be paying in 9 years of premiums beyond the lump sum value that you would get back.
However calculating the benefit of these plans isn’t quite as simple as this – they often provide extra benefits such as extra payouts in the event of dying in an accident or whilst travelling.
An obvious factor to look into is the effects of compound interest when adding the same amount (£6) into a bank savings account every month.
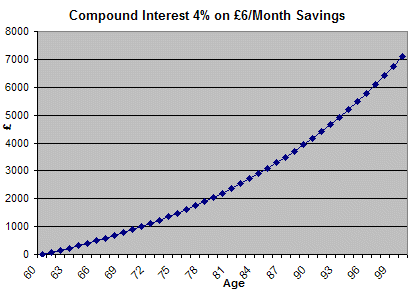
This graph is showing the effect of saving £6 a month based on a modest 4% gross interest rate. I based the calculations to produce this graph on the formula given on patrick schneider blog post. The final figure after 40 years matches the figure given by other compound interest monthly savings calculators I’ve seen on the internet so hopefully the graph is accurate!
Below I’ve put the compound interest curve on top of the previous graph comparing contributions against the cash lump sum.
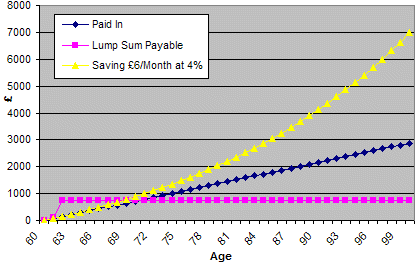
There are further complications to consider such as the effect of inflation. The real worth of any money your family would get back when using these plans is reduced every year due to inflation. On the other hand the real world cost to you goes down each year as your £6 per month will gradually constitute a smaller percentage of your income.
What are my conclusions? I’m not giving you any! Any decision on whether to use a financial product should be taken based on your personal financial circumstances and with the help of a trained financial advisor (which I’m not).
I would say that these are the kind of analyses you should be doing when investigating or comparing any kind of financial product, whether it be a savings account, loan or mortgage. Turning financial information into simple graphs is a very powerful tool that can save you a lot of money!
wish u had been around 18 yrs ago when my mother now 93 took out this £5 mth policy she was so upset to be told she would only ever receive £365 she said she would not give them another penny and has received cancellation value of £199 after paying in over £1000!legal yes -but fair?this policy should come with a health warning DON`T LIVE TOO LONG!