The requests for the 2016 excel staff holiday planning spreadsheet have been coming in so I have made it as well 2017 one. Also I’ve uploaded the 2016/2017 one page excel calendars.
Staff holiday planner
First up here are my free spreadsheet that can help you track staff leave/holiday, training, sick days, offsite days, etc.
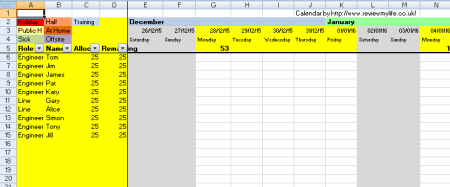
They come set up with formulas that can automatically track the total number of holiday days remaining (columns C&D) for each employee. If you don’t want to use this simply delete those columns.
The default formula subtracts 1 or 0.5 from the remaining holiday if the employee cells contain the words ‘holiday’ or ‘half. You can copy and paste (ctrl-c, ctrl-v) the coloured tags (holiday, half, training, etc) from the top left into the staff planning cells and the totals are automatically updated.
Note that the formulas measure the tags from the very start column (which is the year before) to the very end column (which is the year after).
See the 2012 planner for some customisation examples.
The week numbers are based on ISO 8601, and the top and left parts of the staff planner are frozen so you can always see them – this makes navigation easy. Here is the download link:
Download 2016 staff holiday planner spreadsheet – 22kb
Download 2017 staff holiday planner spreadsheet – 22kb
As the staff holiday planner has over 365 columns you won’t see the whole year if you open it with an old spreadsheet package such as Excel 97. You’ll need to use a more modern spreadsheet package such as Excel 2007 or LibreOffice (which is free). One workaround if you are forced to use Excel 97 at work is for you to use LibreOffice at home to split the spreadsheet into 2, one part for H1, and one for H2.
One page Excel calendar
I’ve put the whole year in this one page Excel spreadsheet.
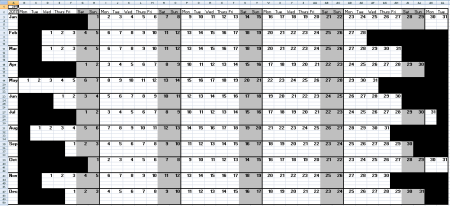
You should be able to load the XLS using any version of Microsoft Excel from 97 onwards, or using the free OpenOffice or LibreOffice.
2016 one page Excel calendar – 13kb
2017 one page Excel calendar – 13kb
The one page Excel spreadsheet calendars and the staff holiday planners are zipped up. If your OS won’t automatically open the zip files you can download the free 7-Zip to unzip them for you.



HI,
Many thanks for your great holiday spreadsheet. Can you please advise me on how to delete a booked holiday, I have tried but I find the total does not change when I delete the cell.
Thanks
Paul.
thanks so much for your planner, you save me so much time every year & it’s much appreciated
Just want to say many thanks for your holiday spreadsheet , Brliant
brilliant tool – very useful – is there any way to send you a small donation for keeping up good work, add to your beer fund or something?
Thanks
Igor
Thanks for the Holiday spreadsheet it’s very useful and has saved me hours of setting up
Thanks for the holiday planner
Simple and highly effective, I have shared this calendar with other managers. Really appreciated, thanks for 2016, until next year
Just want to say many thanks for the holiday planner spreadsheet. Great job and saved me so much time. Much appreciated!!!
Hi,I don’t have much Excel experience so I haven’t fathomed out how to deduct holidays automatically. e.g. 20 days allocated, use 5 (entered on sheet) but it doesn’t deduct from total left. Some help would be appreciated! Many thanks.
PS Last year’s seemed to do it automatically.
If anyone is interested I created a Report sheet which uses a validation lisst based on the employee names on calendar sheet say cell D3.
Use the array below to paste in to a cell i.e. A8 (make sure A8:A30 the cell format is set to custom “mm dddd yy” and user shift & Ctrl & enter to store it, then drag the cell down, say about 30 cells deep.
This will return the dates that someone was off for, you can do the same for any ‘reason’ for being off, just change the text in the middle of the forumal and re-save it with shift & Ctrl & enter drag the cells again to populate other cells.
I named the range for employee names emp_name to make it easier to add new people without needing to redo all the formulas and also renames the main sheet to “2016”
you can end up with a decent report page for an employee which can then be printed.
=IFERROR(INDIRECT(“2016!R5C”&SMALL(IF(INDIRECT(“2016!$A$”&MATCH($D$3,Emp_Name,0)+7&”:$NT$”&MATCH($D$3,Emp_Name,0)+7)=”Holiday”,COLUMN(INDIRECT(“2016!$A$”&MATCH($D$3,Emp_Name,0)+7&”:$NT$”&MATCH($D$3,Emp_Name,0)+7))),ROW(1:1)),FALSE),””)
thank you
Dude – fantastic work! Many thanks for sharing it, fair play to you!
Superb holiday planner. Most helpful. Cheers.
Many thanks for your One page excel calendar most useful
So much quicker than making this myself. Even imports into Google sheets nice and easily. Much thanks
This is fantastic………….will hopefully help me not to mess AL up Thanks
Thank you so much much for your hard work. Is there a way that instead of placing ‘holiday’ one could enter how many hours instead, as some of my staff might only need 3 hours off in a specific day?
Hey, thanks for this great holiday planer. Is it possible that there is more rows? I need more rows, and it seem I cant find the way to insert them? Any solution on this matter will be highly appriciated!
Thanks in advance
Amazing vary helpful. Any formulas to plus a half day. I want this to plus half day to the overall when we work overtime.
Brilliant holiday planner! much appreciated.
Very helpful saves you lots of time
Your holiday planner is an excellent resource and has saved me a heap of time. I was able to combine your 2016 and 2017 planners in minutes and I will have a very happy colleague on Monday morning – thank you.
The formula below should be copied into cell B2 and then dragged to Cells (B2:AL14), with the year entered in A1, “Mon” to “Sun” entered at the top (B1:AL1) and “Jan” to “Dec” entered along the side (A2:A14). Note the days and months must be 3 letters only. Once populated you can insert new lines (e.g. below each month) and will find the formula quite sturdy
=IF(IFERROR(TEXT(A2+1,"mmm"),"")=$A2,A2+1,IF(AND(TEXT("01 "&$A2&" "&$A$1,"ddd")=B$1,COLUMN(B$1)<9),VALUE(TEXT("01 "&$A2&" "&$A$1,"YYYY-MM-DD"))," "))Addendum: I suggest you format the cells to Custom, type “dd”, and apply conditional formatting to the columns of
1) for Cells B1:AL14; cell is blank; fill black
2) for cells B1:AL14;
=OR(B$1="Sat",B$1="Sun"); fill greyHello,
how do i add and delete another employee. If I want to amend an employee, do i have to delete the employee first and then re-insert the employee again?
Regards
Ian
i am a user of your calendar for 3 year and it is very easy to use, you had one column that carry over last year holiday to next year if you can amend or tell me how to add this will appreciate.
Great stuff, thanks man. Been looking for something like this. Will save me lots and serve me lots.
Thanks a lot for this. saved me lots of time that would have been spent making one of these for the manager at work
The 2018 and 2019 calendars are now up here: https://www.reviewmylife.co.uk/blog/2017/01/17/2018-and-2019-staff-holiday-excel-planner-and-one-page-excel-calendar/
Brilliant planners used them for several years now. I have however just spotted an error with the 2018 one page Excel calendar. November starts twice on Thursday and Saturday meaning that it ends on a Sunday when it should end on a Friday.